연속 부분 수열 합의 개수

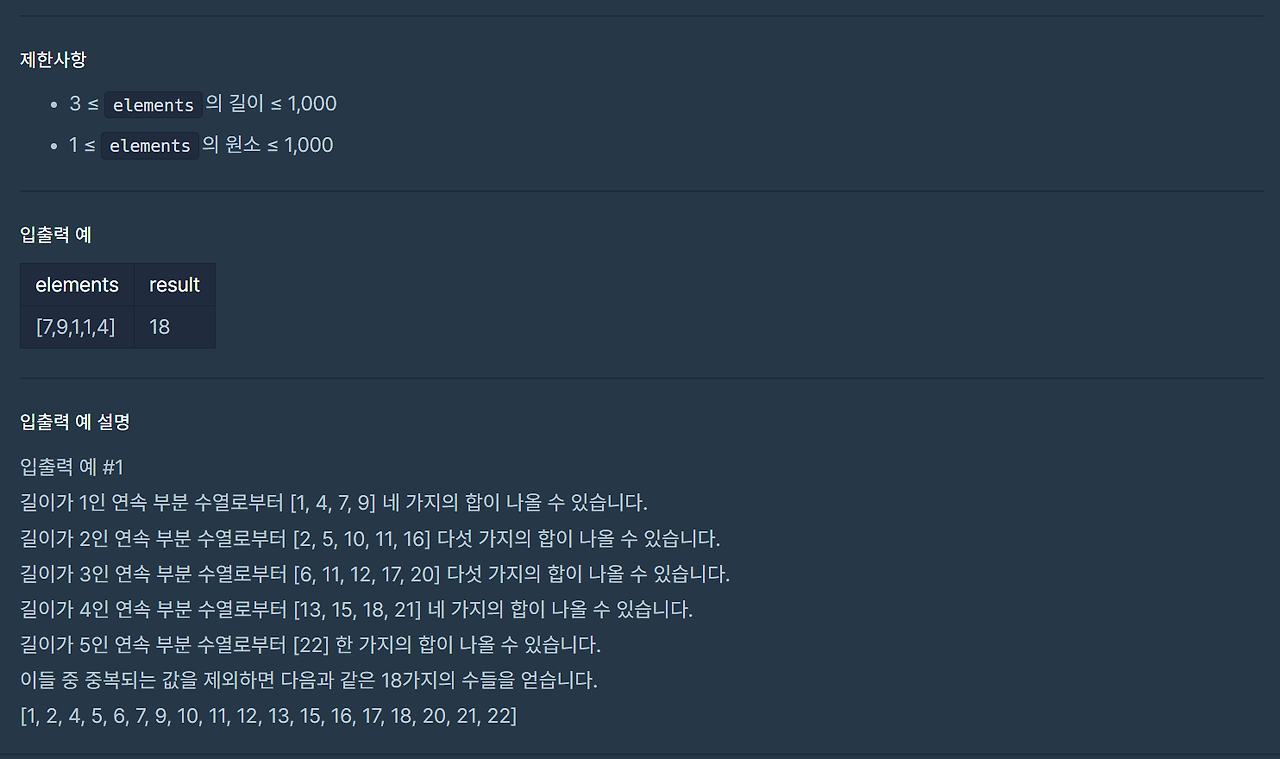
풀이
푸는 것은 어떻게 풀면되겠다는 생각은 들었지만, 맨 끝 인덱스에서 다음 인덱스로 넘어가는 과정에 대해서 고민하는데 시간이 오래 걸렸다.
아래의 코드를 추가하려고 머리를 잠깐 굴렸기 때문이다. 이게 맞나?? 하고 말이다.
if j+i > N:
sum_value += sum(elements[j:])
sum_value += sum(elements[:i+j-N])for 문을 2개를 사용하면서 슬라이싱과 같이 사용했다.
첫번째 for문은 연속하는 갯수인 1~N개에 대해서
두번쨰 for문은 연속하는 갯수에 해당하는 만큼의 합을 구하기 위한 반복문으로 사용했다.
아래처럼 풀이했다.
def solution(elements):
answer = []
N = len(elements)
# 연속하는 갯수 1 ~ N
for i in range(1, N+1):
# 연속하는 갯수에 따른 합 구하기
for j in range(N):
sum_value = 0
if j+i > N:
sum_value += sum(elements[j:])
sum_value += sum(elements[:i+j-N])
else:
sum_value += sum(elements[j:j+i])
answer.append(sum_value)
answer = len(list(set(answer)))
return answer
# [7,9,1,1,4]
# i == 4, j == 3, 3,4, 1,2
# i ==3, j ==3, 3,4, 1
# i ==3, j ==4, 4,1,2
# i == 2, j == 4, 4,1

문제는 풀렸지만 시간이 오래걸렸다.
다른 사람 풀이
res = set()을 초기에 설정하여서 처음부터 값을 집어넣을 때 중복을 제거하는 방식을 이용했다.
나와는 달리 for문을 2번 사용했는데
첫번째 for문에서는 각 원소를 순회하게 하면서, ssum을 정의해서 입력할 값을 넣어두고,
두번째 for문에서 각 원소를 기준으로 1~elements의 길이만큼 합하는 것을 만드는 과정을 거친다.
i+ll로 명명하고 실제로 값을 이용할때는 elements[j%11] 로 하여 모듈러 연산자를 이용해서 값을 더할 수 있게 만들었다.
(이런방법이!!!!)
이렇게 2중 for문을 돌고나면 res는 이미 중복제거된 것이므로 res의 길이를 반환해주기만 하면된다.
def solution(elements):
ll = len(elements)
res = set()
for i in range(ll):
ssum = elements[i]
res.add(ssum)
for j in range(i+1, i+ll):
ssum += elements[j%ll]
res.add(ssum)
return len(res)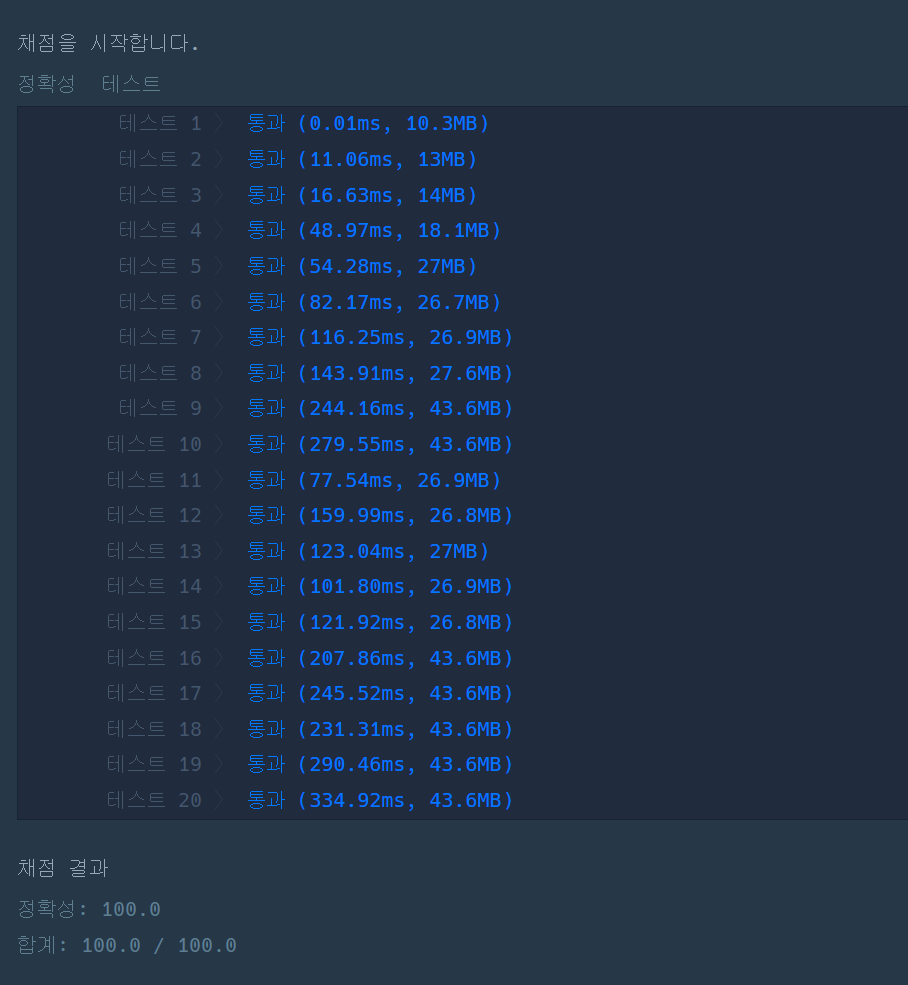
시간차이가 엄청나게 차이가 난다... 나도 똑똑해질래ㅜㅡ
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| python으로 로또 번호 뽑기 (0) | 2024.02.17 |
|---|---|
| 프로그래머스 Lv2 전력망을 둘로 나누기 (python) (0) | 2024.02.16 |
| 프로그래머스 Lv2 가장 큰 수 도움말 (python) (0) | 2024.02.15 |
| 프로그래머스 Lv1 햄버거 만들기 (python) (1) | 2024.02.14 |
| 프로그래머스 Lv1 [PCCP 기출문제] 1번 / 붕대 감기 (python) (0) | 2024.02.14 |



